Interdisciplinary seminar | 16 April 2025

Обзор исследований по построению решений волнового уравнения, локализованных в том или ином смысле. Во-первых, это многоцикловые  импульсы, имеющие локализацию гауссовского типа, во вторых — однонаправленные малоцикловые.

Будем рассматривать класс задач, описываемых уравнениями типа Шредингера

(1)  

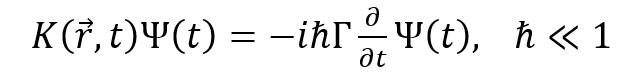
где матрица Γ и оператор K(r,t)  — самосопряженные. Это уравнение Шредингера с несамосопряженным гамильтонианом. Точки вырождения (моменты пересечения уровней энергии) бывают разных видов: могут вырождаться только уровни, может оказаться, что и соответствующие собственные функции вырождаются (исключительные точки). Будут приведены аналоги формул Ландау-Зинера в некоторых случаях (I. Fialkovsky, M. Perel. J Math Phys, 61(4), 2020 ). В уравнении (1) в роли t может быть координата. Примеры применения: Туннелирование через барьер в графене с учетом магнитного поля (готовится к печати). Возможный пример: перевозбуждение ТМ и ТЕ плазмонов на гладкой изогнутой поверхности метаматериала.

Будет рассмотрено несколько задач, в которых волновые процессы описываются уравнением Гельмгольца или “параболическим уравнением” Леонтовича—Фока с негладкими коэффициентами (например, функцией-ступенькой Хевисайда, дельта функцией). К ним относятся, в частности, высокочастотная дифракция на контуре со скачком кривизны и параксиальное распространение волн вдоль тонкого слоя. Строятся асимптотические решения этих задач.

Исключительные точки и объемная дуга Ферми, соединяющая их, возникает, когда в эрмитову систему вносят излучательные потери, заставляя точку Дирака разделяться на две исключительные точки, где как собственные значения, так и собственные функции объединяются. Эффект, экспериментально не показанный ранее на одиночном диэлектрическом резонаторе, был предсказан и описан с помощью квазинормальных мод, что в нашей работе стало основой в экспериментальной реализации.

В работе исследуется модель взаимодействия двух электронов в краевых состояниях двумерного топологического изолятора. Рассмотрены как решения уравнения Шредингера, так и решения уравнения Бете-Солпитера при различных значениях энергии Ферми. Показано, что для уравнения Бете-Солпитера, учитывающего существование поверхности Ферми, в системе двух электронов имеется дискретный спектр. Это явление не проявляется в случае уравнения Шредингера.

Одним из методов возбуждения нелинейных волн в микрорезонаторах является использование рамановского усиления, возникающего при накачке резонатора когерентным излучением. Наличие керровской нелинейности может приводить к модуляционной неустойчивости и образованию частотной гребенки. В докладе обсуждается ситуация, когда нелинейная структура, возникающая в результате развития такой неустойчивости, находится в черенковском синхронизме с полем накачки.