Курс Нелинейные колебания и волны посвящен целому классу явлений, описание которых не сводится к приближениям, лежащим в основе всех привычных соотношений физики. Как правило это побочные эффекты, пренебрежимо малые на фоне основных, описываемых линейными законами. Однако, при некоторых условиях эти эффекты могут выходить на передний план, что приводит к поведению системы, на первый взгляд, удивительному и необъяснимому. Более сложные и тонкие, они могут как возникать сами, так и создаваться специально с целью решениях тех или иных технических задач. Современный специалист в области радиофизики должен знать признаки нелинейного поведения наблюдаемых им систем, уметь описывать и анализировать его, а также владеть арсеналом средств, предоставляемых его целенаправленным использованием. Также в курсе затрагиваются вопросы перехода к хаосу детерминированных систем и самоорганизации (самоусложнения) открытых систем, являющиеся сугубо нелинейными процессами.
Часть I. Динамические системы и их изучение посредством фазового пространства
- Основные определения. Классификация динамических систем. Динамические системы. Стационарное решение. Условие устойчивости.
- Общее рассмотрение устойчивости состояния равновесия автономной системы. Процедура линеаризации.
- Понятие фазового пространства. Особые точки фазового портрета линейной автономной системы второго порядка: седло, узел, центр, фокус; сводная диаграмма.
- Устойчивость состояний равновесия маятника.
- Достаточные условия устойчивости периодического решения (теоремы Ляпунова и Андронова-Витта).
- Отрезок (поверхность) без контакта. Функция последования. Неподвижная точка отображения Пуанкаре.
- Устойчивость неподвижной точки одномерного отображения. Диаграммы Кенигса-Ламерея ("лесенки Ламерея"). Теорема Кёнигса.
- Устойчивость предельного цикла автономной нелинейной системы 2-го порядка.
- Устойчивые и неустойчивые многообразия особых точек, периодических и квазипериодических решений динамических систем. Размерности многообразий
- Устойчивые и неустойчивые (в том числе седловые) состояния равновесия, периодические и квазипериодические движения. Тороидальные интегральные многообразия.
Часть II. Бифуркации динамических систем
- Понятие бифуркации. Бифуркационные диаграммы. Седлоузловая бифуркация. Бифуркация типа вил. Бифуркация Андронова-Хопфа (рождение предельного цикла). Бифуркация удвоения периода цикла.
- Туннельно-диодная схема: основные соотношения, состояния равновесия, их бифуркации и исследование их устойчивости.
- Теорема Пуанкаре-Бендиксона. Получение и анализ фазового портрета туннельно-диодной схемы, обоснование наличия в ней предельного цикла. Предельный цикл при малой ёмкости. Томсоновские и релаксационные колебания.
- Неподвижные точки, мультипликаторы и области значений параметра, соответствующие устойчивым циклам различных периодов. Бифуркации тороидальных интегральных многообразий.
Часть III. Приближенные методы анализа динамических систем
- Общие положения и условия применимости. Четыре метода. Метод гармонического баланса – идея метода.
- Исследование установившихся колебаний квазилинейного осциллятора Рэлея методом гармонического баланса.
- Осциллятор Дуффинга. Механическая модель. Исследование воздействия гармонической силы методом гармонического баланса.
- Метод малого параметра – идея метода. Резонанс второго рода: понятия и определения.
- Анализ свободных колебаний маятника без потерь методом малого параметра.
- Общие черты процедуры метода Ван дер Поля для квазилинейной системы 2-го порядка
- Метод медленно меняющихся амплитуд. Идея метода, предварительные процедуры, составление укороченных уравнений
- Процессы установления и устойчивость установившихся колебаний автономного LC–генератора
- Резонансное воздействие источника гармонических колебаний на LC – генератор (главный резонанс). Двухконтурный генератор.
Часть IV. Фазовые пространства и точечные отображения в случае неавтономных систем
- Линейные системы, находящиеся под воздействием периодической силы. Неавтономный линейный осциллятор.
- Нелинейный осциллятор. Гомоклиническая структура. Гетероклиническая структура. Неустойчивость по Ляпунову и устойчивость по Пуассону. Понятие «странного» аттрактора.
- Переход к хаосу через последовательность удвоений периода колебаний (временные диаграммы, фазовые портреты, спектрограммы). Система Рёсслера и её аттрактор.
- Сценарий перехода к хаосу через перемежаемость. Другие механизмы стохастизации динамических систем.
Часть V. Размерность стохастических множеств
- Понятие фрактальной размерности (по КолмогоровуХаусдорфу). Канторово множество, кривая Хельге фон Коха. Размерность ломаной, аппроксимирующей береговую линию.
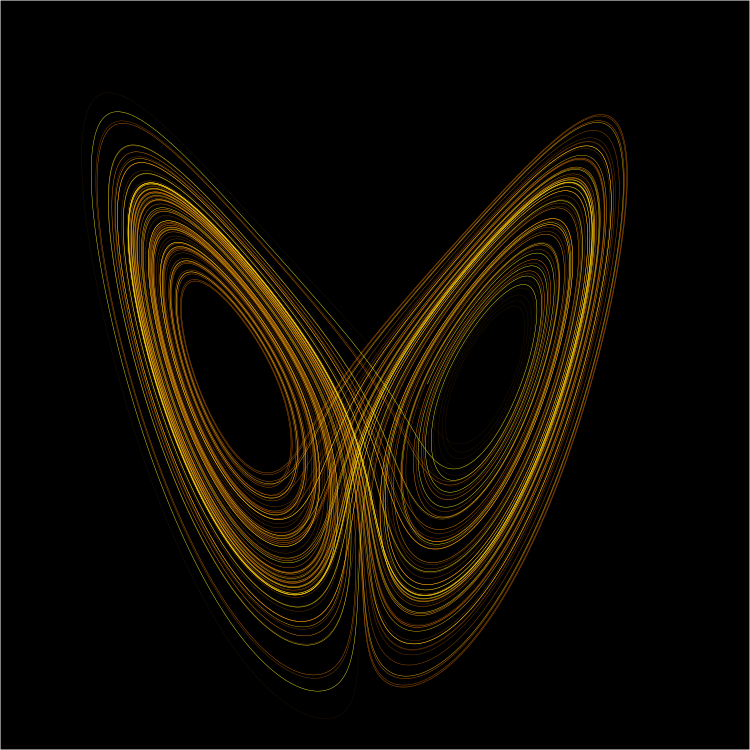
- Масштабная инвариантность ("самоподобие") канторова множества. "Канторовость" структуры странных аттракторов. Фрактальная размерность аттрактора Лоренца
Часть VI. Регулярные и хаотические колебания в распределенных системах
- Нелинейная распределенная система без потерь и дисперсии. Решение в виде ударной волны: исходные соотношения и допущения, анализ возможных решений.
- Генерация второй гармоники при распространении света в нелинейной среде. Турбулентность как динамический хаос в распределенной системе.
Дополнительная тема: Механизмы самоорганизации в открытых системах
- Системы большого числа частиц. Определение самоорганизации. Закрытые и открытые системы. Интегральный лагранжиан механической системы без трения. Системы с сильным трением. Понятие динамической работы. Динамические структуры: механизм рождения, старения и гибели. Динамический хаос как предел эволюции динамических систем. Распространение принципов на биологические и социальные объекты. Возникновение и эволюция живых форм. Дерево бифуркаций.



